Transformaciones en el plano y el plano cartesiano
transformaciones geométricas:
Transformaciones en el plano:
son procesos de variación o movimiento de los puntos del plano de forma que se establece una relación entre los elementos de origen y los elementos transformados. diremos que un par de puntos son homólogos cuando se obtenga mediante la aplicación de una transformación en su plano.
puede ser 2 tipos:
transformación directa: se conversan el sentido en el plano orientado.
transformación inversa: cuando los sentidos del original y el homologo son contrarios .
También la podemos clasificar en función al aspecto de la figura homologa en:
isometricas: son aquello que conversan las dimensiones y los ángulos entre la figura original y la transformada.
- traslación
- giro
- simetría
isomorficas o conformes: son aquellas transformaciones que conservan la forma, es decir, los ángulos de la figura original y la transformada son iguales y las longitudes son proporcionales.
- homotecia
- semejanza
anamorficas: son aquellas en las que cambia la forma entre la original y la transformada.
-inversión
transformaciones isometricas:
en geometría, las transformaciones isometricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones ni el área de las mismas; la figura inicial y la final son semejantes y geometricamente congruentes.
la palabra isometria tiene su origen en el griego iso (igual o mismo) y metria (medir), una definición cercana es igual medida.
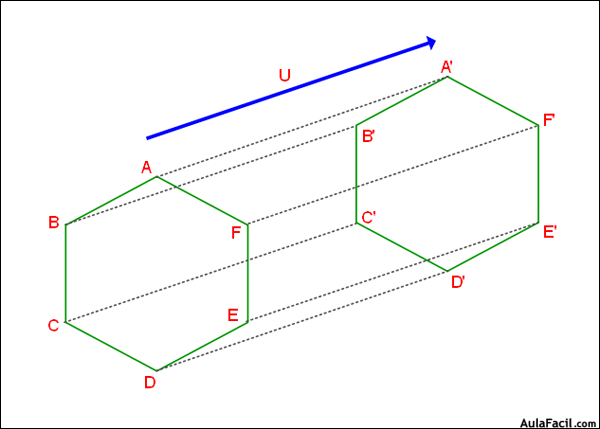
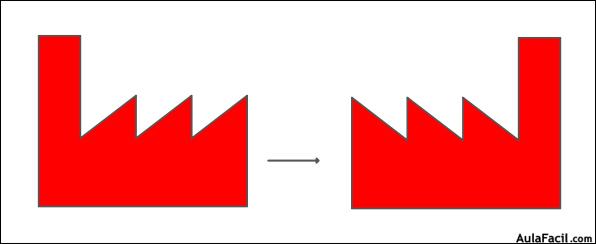
Traslación: la traslación es una isometria que realiza un cambio de posición, es el cambio de lugar, determinado por un vector.
se llama traslación de vector a la isometria que a cada punto A del plano le hace corresponder un punto A' del mismo plano tal que AA' es igual a U vector
-la dirección: si es horizontal, vertical, oblicua, etc...
-el sentido: si es derecha, izquierda, arriba o abajo.
-la magnitud: que se refiere a cuanto se desplazo la figura en una unidad de medida.
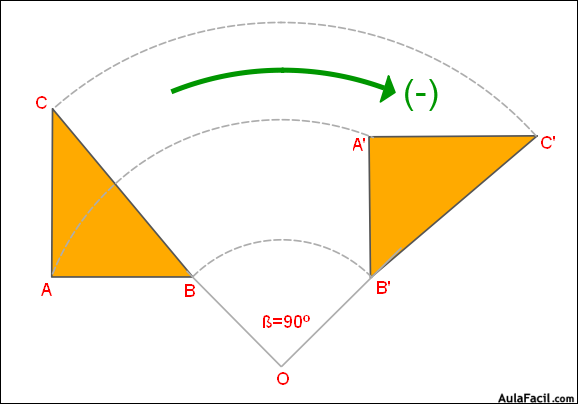
giro: una rotación, en geometría, es un movimiento de cambio de orientación de un cuerpo, de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y posee las siguientes características:
-un punto: denominado centro de rotación
-un angulo
-un sentido: de rotación
estas trasformaciones pueden ser positivas o negativas dependiendo del sentido de giro. para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y sera negativo el giro cuando sea en sentido de las manecillas.
se denominan: central y axial
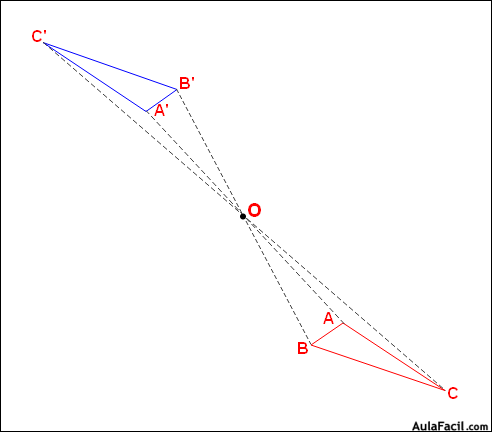
simetría central:es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:
- el punto y su imagen y el centro de simetría pertenezca a una misma recta
.
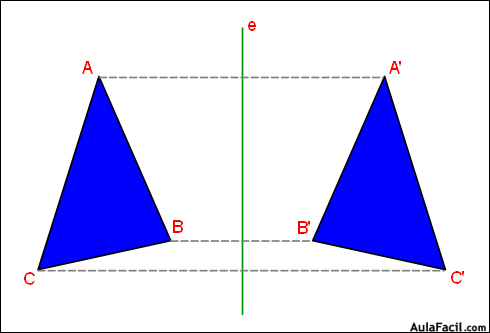
transformaciones isomorficas: son las transformaciones geométricas que solo conservan la forma; es decir, en aquellas los ángulos de la figura original y de la transformada son iguales y las longitudes proporcionales.La simetría axial, en geometría, es una transformación respecto de un eje de simetría, en la cual, a cada punto de una figura se asocia a otro punto llamado imagen, que cumple con las siguientes condiciones:
- La distancia de un punto y su imagen al eje de simetría, es la misma.
- El segmento que une un punto con su imagen, es perpendicular al eje de simetría.
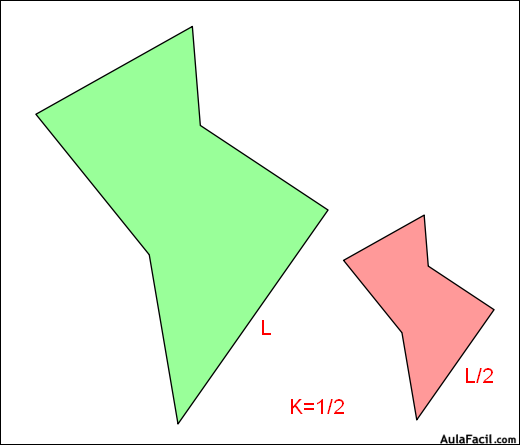
semejanza: dos figuras son semejantes cuando tienen la misma forma (el mismo numero de lados y ángulos iguales) y de distintos tamaños (sus dimensiones son distintas).
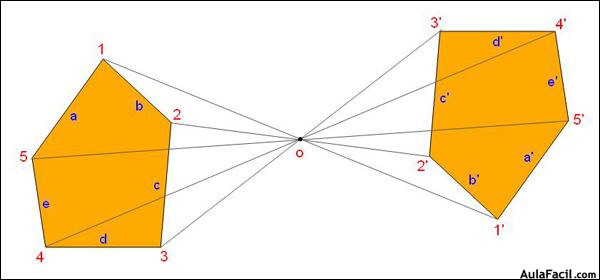
la homotecia: es una transformación geométrica, una correspondencia entre 2 figuras en la que se cumple que las parejas de puntos homoteticos están alineados con el centro de homotecia y los segmentos homoteticos son paralelos.
.
Las figuras homotéticas directas son semejantes y nunca son equivalentes. homotecia inversa:Cuando los puntos homotéticos se encuentran alineados con el centro pero en extremos opuestos de las radiaciones, la homotecia es inversa.En este caso la figura no es semejante, es el producto de dos simetrías axiales cuyos ejes, uno vertical y otro horizontal pasan por el centro de homotecia.
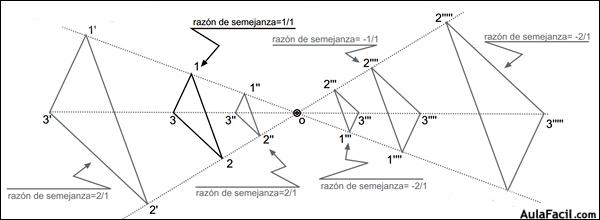
Factor de proporcionalidad de la homotecia:
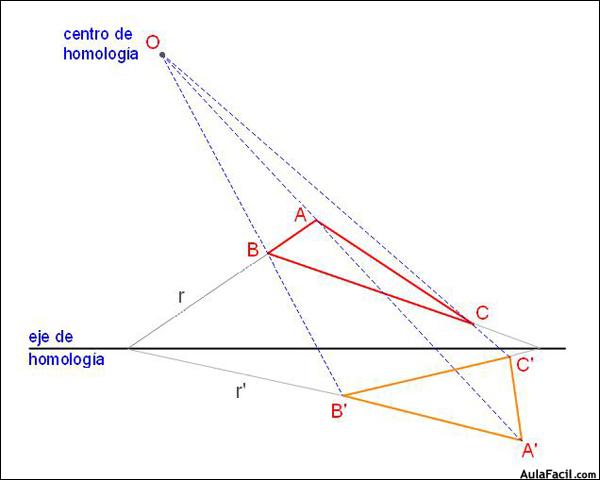
La homología es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de las figuras.transformaciones geométricas anamorficas:
- Dos puntos homólogos A y A’ están alineados con un punto fijo, que es el centro de la homología.
- Dos rectas homólogas r y r’ se cortan en una recta llamada eje de la homología.
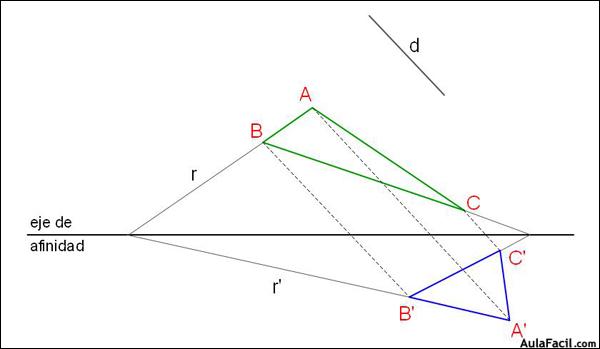
afinidad:La afinidad es una homología con el centro en el infinito. Es una transformación que no es isomórfica ni isométrica, pues no mantiene la forma ni el tamaño de la figura que transforma.
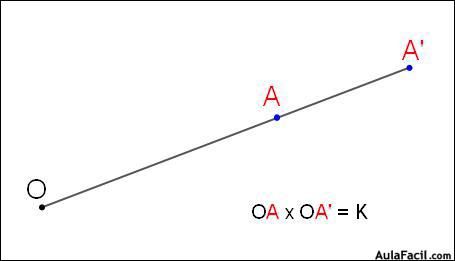
Inversión:La inversión es una transformación que hace corresponder a un punto A otro punto A’ cumpliendo las siguientes condiciones :
El Plano
Cartesiano:
El
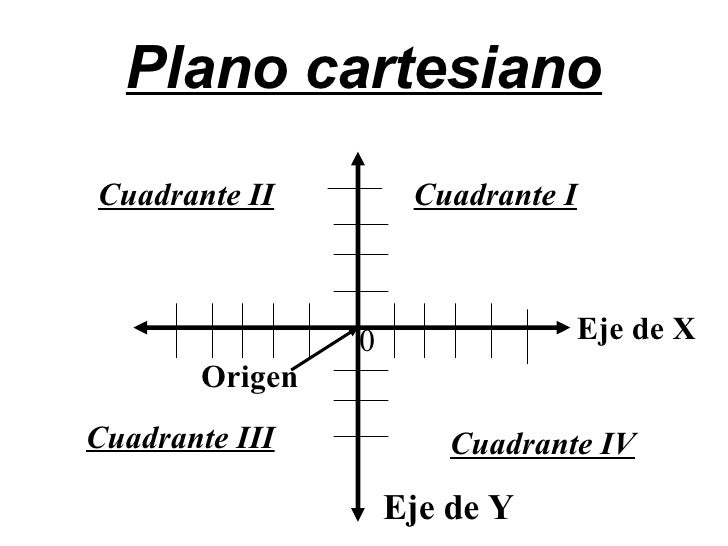
plano cartesiano es un sistema de referencias que se encuentra conformado por
dos rectas numéricas, una horizontal y otra vertical, que se cortan en un
determinado punto. A la horizontal se la llama eje de las abscisas o de las X y
al vertical eje de las coordenadas o de las Yes, en tanto, el punto
en el cual se cortarán se denomina origen. La principal función o finalidad de
este plano será el de describir la posición de puntos, los cuales se
encontrarán representados por sus coordenadas o pares ordenados. Las
coordenadas se formarán asociando un valor del eje X y otro del eje Y.
En tanto, para localizar los puntos en el plano
cartesiano se deberá tener en cuenta lo siguiente… para localizar las abscisas
o valor de las X, se contarán las unidades correspondientes en dirección
derecha, si son positivas y en dirección izquierda, si son negativas, partiendo
del punto de origen que es el 0. Y luego, desde donde se localizó el valor de X, se procederá a contar las unidades correspondientes hacia arriba en caso de
ser positivas, hacia abajo, en caso de ser negativas y de esta manera se
localiza cualquier punto dada las coordenadas. La distancia que separa el lugar
desde donde nosotros nos hayamos, hasta por ejemplo el lugar al cual nos
queremos dirigir, que, supongamos queda a cuatro cuadras al norte y seis al
oeste, puede ser plasmada a través de un plano cartesiano, tomando como origen
del plano aquel en el cual nos encontramos nosotros.
El origen de la denominación de plano cartesiano como tal se ha efectuado en
honor al reconocido matemático y filósofo francés del siglo XVII René
Descartes, por haber promovido la necesidad de tomar un punto de partida sobre
el cual edificar todo el conocimiento.

felicitaciones por su aporte
ResponderBorrar